Note: the text below is an adaptation and simplification of the content from a number of lectures in which I either introduced the concept of complexity analysis, or connected it to other topics (such as specific algorithms and data structures). These lectures were given in Portuguese, and what follows is not a direct translation. Rather, it is a sample of some of the essential insights gathered from the experience of explaining the topic to hundreds of students.
Complexity Analysis
Or: finding out how good an algorithm is
Complexity analysis is the process of finding out, for example, how fast an algorithm is. It has other uses, such as estimating how much memory an algorithm needs, but speed is what’s most commonly talked about.
Why do we need it?
Now you might be thinking: why do we need something with a fancy-sounding name just to know how fast an algorithm is? Can’t we just run a piece of code, time it, and find out exactly how fast it is?
Well, we could. But there are some problems with doing that.
The first (and biggest) issue is that the time a code takes to run depends on a number of factors. It depends on the language used to implement the algorithm, how powerful is the computer used to run it, what is happening with other programs running at the same time (including the OS), and many other factors that have nothing to do with the algorithm itself.
Besides, what if we wanted to compare different algorithms, perhaps ones that were created by different people in different places and even at different moments in time? To be able to compare which one is faster, we would need to run their code equivalent under exactly the same conditions, otherwise the comparison wouldn’t be fair or even meaningful.
And that’s the motivation behind complexity analysis: evaluating and comparing algorithms in a way that is meaningful and consistent, independently of any code being executed.
Same problem, two different algorithms
Suppose we want to write an algorithm to find the largest number in a list. Let’s see two different approaches to this problem, and then compare them.
Note: here I’m writing the algorithms in Python just to express them in some way, but remember that the idea is to be able to analyze them independently of the concrete implementation. In fact, they could just as well be written in pseudo-code, I just prefer Python.
Here’s version A (to make our lives easier, let’s assume the input list is not empty):
def find_max_version_A(numbers):
largest = numbers[0]
for num in numbers:
if num > largest:
largest = num
return largest
We start by saying that the largest number is the first in the list (we are assuming the list is not empty). Then we proceed and check all numbers in the list to see if there is one even larger. Whenever we find a larger one, we consider that one as the new largest. When we get to the end of the list, we can just return the largest one we found.
Now take a look at version B:
def find_max_version_B(numbers):
for candidate in numbers:
is_largest = True
for num in numbers:
if num > candidate:
is_largest = False
if is_largest:
return candidate
In this version, the idea is that we take each number of our list as a candidate for the largest one, and then check if in fact it is the largest. If there is any number larger, then we know the candidate is not the largest. But if no number is larger, then we have found the largest one.
Which one is faster?
Looking at the algorithms, do you have a hunch on which one is faster? If not, take a look at them again and think about it, even if you don’t know exactly why you would choose one over the other.
If you said algorithm A is the faster one, you are correct (we’ll understand why soon). But don’t worry if you chose version B. It’s not always obvious which algorithm is faster, especially if we need a stricter way of arguing for it.
And here’s where complexity analysis comes into play. Some people might choose A as the faster one because it has only one for loop, while version B has two. In a sense, version B seems more “complicated”, even if just for having more code.
But that alone is not enough to judge. There are some very fast algorithms that use techniques that might seem “complicated” at first.
Complexity analysis is not about how complicated an algorithm seems, nor about how long it is. The word “complexity” in this case has a very specific meaning, which has to do with how the algorithm behaves when we change its input size.
What happens when we go bigger?
As mentioned in the beginning, complexity analysis has multiple uses, but the most common one is about evaluating the speed of an algorithm. The precise way to do that is to establish a relation between the size of an input and how many operations an algorithm takes to solve the problem.
In other words, we are not interested in how long the algorithm takes to run in a particular case, but in how the number of operations changes as we change the input size.
To represent the size of the input (e.g. the number of items in a list), it is customary to use the letter $n$. Let’s take a look at our algorithms, but now counting how many operations each needs.
Here’s version A, commented:
def find_max_version_A(numbers):
largest = numbers[0] # 1 operation
for num in numbers: # this loop executes n times
if num > largest: # 1 operation
largest = num # 1 operation
return largest # 1 operation
The first question we need to ask ourselves is: what counts as an operation? The answer is that it can be complicated, and might vary from case to case. But for our purposes, we count as an operation things like a comparison, an assignment, a return, a calculation, etc.
Another important thing to notice is that, even if a line of code has only one operation (such as an assignment), it might be executed multiple times.
In our case, the first and last lines of the function (an assignment and a return) are executed only once. However, the operations that are inside the for loop (comparison and assignment) will be executed a number of times that depends on the size of our input.
So, assuming $n$ is the number of items in our input list, the total number of operations of algorithm A will be:
- 2 fixed operations (first assignment, and return at the end)
- 2 operations in the loop, times $n$ iterations
This gives us a formula (i.e. a mathematical expression or function) for calculating the number of operations: $2 + 2*n$ or, equivalently: $2n + 2$.
Note that the formula does not really depend on the technical and concrete details of an execution of the code. Rather, it depends only on the structure of the algorithm.
Now let’s do the same for version B:
def find_max_version_B(numbers):
for candidate in numbers: # this loop executes (at most) n times
is_largest = True # 1 operation
for num in numbers: # this loop also executes n times
if num > candidate: # 1 operation
is_largest = False # 1 operation
if is_largest: # 1 operation
return candidate # 1 operation
Most aspects are similar between this and the previous case. But version B has an interesting twist: a loop inside a loop. That means that for each of the $n$ iterations of the outer loop, the inner loop will also execute $n$ times.
Since we don’t have any fixed number of operations outside the loops, what we can do is analyze first what happens in a single iteration of the outer loop:
- 3 operations (assignment at the beginning, plus comparison and return at the end)
- 2 operations times $n$ iterations of the inner loop
But that happens for each iteration of the outer loop, which itself also executes $n$ times (at most). So in the end we have: $(3 + 2*n) * n$ or, equivalently: $2n^2 + 3n$.
Comparing the algorithms
Now, to compare how fast both algorithms are, we can use the formulas we found. If we plot them both on a graph, this is what they would look like:
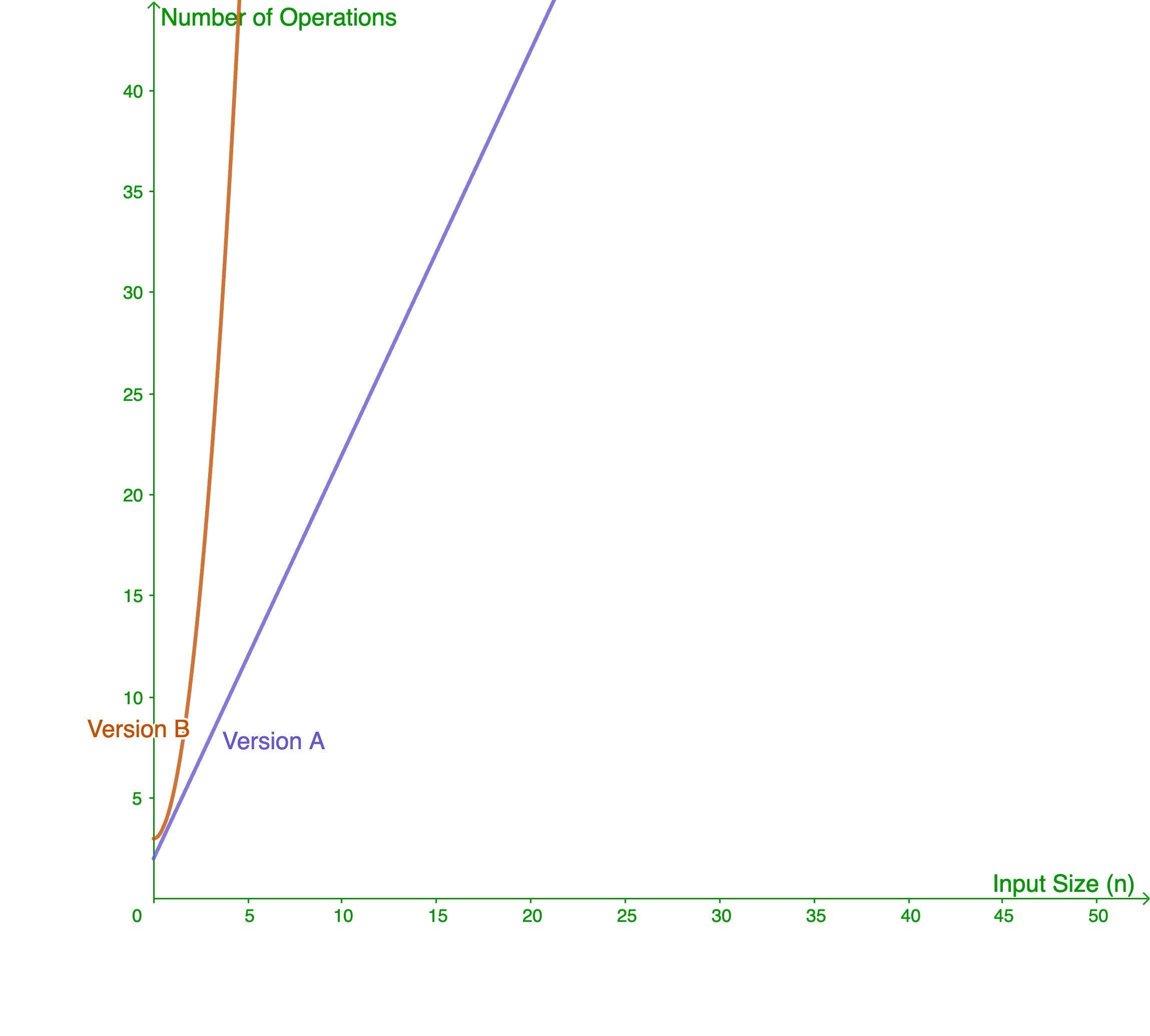Notice how the graph clearly shows that, as the input size increases, the algorithms require a significantly different number of operations. Even if for small input sizes they are very similar, version B grows much more rapidly (uses more operations) than version A, which means that indeed version A is faster (uses fewer operations).
It is important to understand that what matters is not so much the exact number of operations each algorithm takes (although that can be useful sometimes). What matters most is how they behave as our input size grows. Because of that, we don’t really need the exact formula for each algorithm. All we need is a way to represent how fast they grow.
In this type of analysis, we often use what is called an asymptotic notation for the complexity. Asymptotic just means something like “how it behaves on the limit”.
Big-O notation
There are multiple possible asymptotic notations for different cases, but one that is particularly common and useful is the big-O notation. The big-O notation (and other asymptotic notations) simplifies the mathematical expression in our formula for calculating the number of operations, taking just the parts that affect it the most. In particular, the big-O notation gives an upper bound for our algorithm, meaning “the behavior will not be (much) worse than this”. Often we care just about the worst case scenario for an algorithm, which is why the upper bound is commonly used.
Let’s go through each version once more.
For version A, the complete mathematical expression for the number of operations is $2n + 2$. But notice that what matters most here is the $n$. The constant $+ 2$ doesn’t really affect the behavior, it wouldn’t matter if it were 3 or 5 or 10 operations initially. But even the factor $2$ that is multiplied by $n$ does not matter that much. What matters is that for each increase in the input size $n$, the number of operations needed grows linearly, that is, in a linear relationship with $n$.
In big-O notation we represent that time complexity with $O(n)$. In English, we say it “time complexity big O of n”, or simply “linear time complexity”.
For version B, our full mathematical expression for the time complexity is $2n^2 + 3n$. But we also can discard a bunch of these things, as we only care about the asymptotic behavior. Between $2n^2$ and $3n$, the first part dominates the function, which means that in the end the second part does not matter that much, and we can discard it. Similarly to before, the factor $2$ of $2n^2$ also does not matter that much.
So in big-O notation we represent that time complexity with $O(n^2)$. In English, we say it “time complexity big O of n squared”, or simply “quadratic time complexity”.
Linear and quadratic complexities are very common, but there are many others. Here’s a list of commonly used ones (listed in increasing order of how fast they grow):
- Constant: $O(1)$
- Logarithmic: $O(\log{n})$
- Linear: $O(n)$
- Linearithmic: $O(n \log{n})$
- Quadratic: $O(n^2)$
- Cubic: $O(n^3)$
- Exponential: $O(a^n)$
- Factorial: $O(n!)$
For common algorithms (including operations with specific data structures), there are usually documented complexity analyses of how fast they are. But there is no substitute for practice, so we recommend that you develop the mindset of trying to understand (and research, if necessary) the time complexity of any algorithm you encounter, including your own!
Recapitulating
Now let’s put everything together, from the beginning. When we want to know how fast an algorithm is (or compare multiple ones), we can do an analysis about its time complexity. We achieve that by evaluating how the number of operations of the algorithm changes as we increase its input size.
But we often don’t care about exactly how many operations it takes, just its general behavior. That’s why we can use asymptotic notations such as big-O, which gives us an upper bound for how fast the number of operations can grow. That is often enough to grasp which algorithm is better suited to solving a given problem.